Merge Sort
Merge-Sort é um algoritmo para ordenação de dados simples e compacto, normalmente implementado utilizando recursão. A idéia do Merge-Sort é embasada na divisão de um vetor, dividi-lo em vários vetores menores até que não se possa dividir mais. Depois compara-se os elementos dos vetores menores para uni-los na ordem desejada.
O Merge-Sort é baseado em um padrão de projeto chamado divisão e conquista (divide-and-conquer), que pode ser dividido em 3 partes:
- Divisão: Se a quantidade de elementos que serão ordenados for um ou dois então resolva o problema diretamente, se tiver mais elementos então divida a quantidade de elementos em dois ou mais conjuntos.
- Recursão: Utilize a recursão para resolver cada um dos subconjuntos de elementos.
- Conquista: Depois da resolução de cada subconjuntos, reagrupe-as em uma única solução.
Fluxo de execução do Merge Sort
Dado um vetor de elementos inteiros [3, 5, 4, 1, 9, 6, 7, 2], ordená-lo utilizando Merge Sort. Divide o vetor até ter um par de elementos, ordena esses elementos e altera a ordem deles no vetor original se necessário:
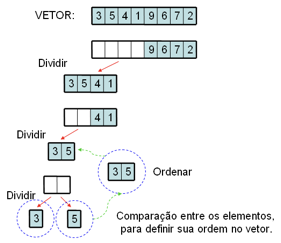
Ordena outro par de elementos e altera a ordem deles no vetor original se necessário:
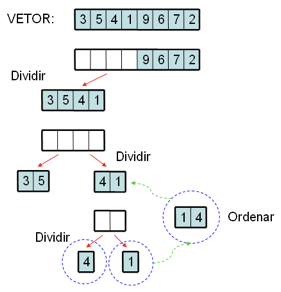
Depois que tem 2 pares ordenados, ordena este 2 pares e altera a ordem deles no vetor original se necessário:
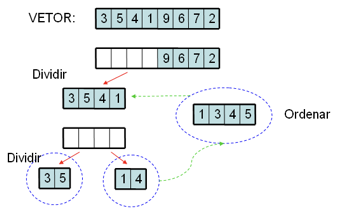
Continua ordenando a outra metade do vetor, faz o mesmo processo de dividir os elementos até chegar em um par de valores e ordena esses valores e altera a ordem deles no vetor original se necessário:
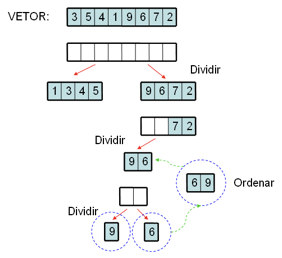
Ordena outro par de elementos e altera a ordem deles no vetor original se necessário.

Depois que tem 2 pares ordenados, ordena estes 2 pares e altera a ordem deles no vetor original se necessário:

Depois que as duas metades do vetor está ordenado, ordena novamente as duas metades e altera a ordem dos elementos no vetor original se necessário:

O vetor foi ordenado por completo:

Implementação do Merge Sort iterativo
package mergesort;
public class MergeSort {
public static void main(String[] args) {
//Cria um vetor de inteiros e atribui os valores.
int[] numeros = {3, 9, 8, 7, 6, 2, 1};
//Chama o método que vai executar o algoritmo do Merge Sort.
mergeSort(numeros.length, numeros);
//Imprime os valores do vetor após ser ordenados pelo Merge Sort.
for(int x : numeros) {
System.out.print(x + " ");
}
}
/**
* Método que ordena um vetor de elementos inteiros, utilizando o algoritmo
* do Merge Sort.
*
* @param tamanho - Tamanho do vetor.
* @param vetor - Vetor de números inteiros.
*/
private static void mergeSort(int tamanho, int[] vetor) {
/* Variavel utilizada para percorrer o vetor.
Inicializa com 1 para indicar que o vetor tenha pelo menos 1 elemento. */
int elementos = 1;
/* Variaveis utilizadas para marcar o inicio, meio e fim do vetor. */
int inicio, meio, fim;
/* Percorre os elementos do vetor até chegar no fim do vetor. */
while(elementos < tamanho) {
/* Aponta o inicio do vetor. */
inicio = 0;
/* Percorre o vetor do inicio + quantidade de elementos ja percorrido,
até o tamanho do vetor. */
while(inicio + elementos < tamanho) {
/* Guarda a posição do meio do vetor que será ordenado. */
meio = inicio + elementos;
/* Guarda a posição final do vetor que será ordenado. */
fim = inicio + 2 * elementos;
/* Caso o fim fique com um tamanho maior, que o tamanho do vetor,
então faz o fim ter o mesmo tamanho que o tamanho do vetor. */
if(fim > tamanho)
fim = tamanho;
/* Chama o método que faz a intercalação dos valores
ordenados do vetor. */
intercala(vetor, inicio, meio, fim);
/* Faz o inicio do vetor ser igual ao fim. */
inicio = fim;
}
/* Percorre o vetor dobrando a quantidade de itens ja ordenados. */
elementos = elementos * 2;
}
}- Na linha 24 tem a assinatura do método mergeSort no formato iterativo, que recebe o tamanho do vetor e o vetor que será ordenado.
- Na linha 27 é criado uma variável para percorrer os elementos do vetor, está variável é inicializada com 1 porque o vetor precisa ter pelo menos um elemento dentro dele.
- Na linha 29 é criado três variáveis para controlar a posição inicial, meio e fim do vetor que será trabalhando.
- Na linha 32 é criado um while para percorrer todos os elementos do vetor, neste while o vetor será percorrido de 1 em 1, depois de 2 em 2, depois de 4 em 4, etc, porque estamos simulando o tamanho do vetor original, para dividi-lo em partes pequenas que podem ser ordenadas e depois intercalada.
- Na linha 38 é criado outro while para percorrer os elementos do vetor, utilizando a quantidade de elementos de 1 em 1, de 2 em 2, ou seja, vai ordenar dois elementos ou quatro elementos ou oito elementos.
- Na linha 40 define qual a posição do meio do vetor.
- Na linha 42 define qual a posição final do vetor.
- Na linha 51 chama o método que intercala os valores do vetor, de acordo com as posições inicio, meio e fim passadas.
- Na linha 54 faz a posição inicial do vetor ser igual a posição fim, porque será ordenado outra parte do vetor.
- Na linha 58 duplica o tamanho dos elementos que deve ser ordenados e intercalados.
/**
* Método responsavel por intercalar os valores do vetor de forma ordenada.
*
* @param vetor - Vetor que terá seus valores ordenados.
* @param inicio - Posição inicial da ordenação no vetor.
* @param meio - Posição do meio da ordenação no vetor.
* @param fim - Posição final da ordenação no vetor.
*/
private static void intercala(int[] vetor, int inicio, int meio, int fim) {
/* Vetor utilizado para guardar os valors ordenados. */
int novoVetor[] = new int[fim - inicio];
/* Variavel utilizada para guardar a posicao do inicio do vetor. */
int i = inicio;
/* Variavel utilizada para guardar a posição do meio do vetor. */
int m = meio;
/* Variavel utilizada para guarda a posição onde os
valores serão inseridos no novo vetor. */
int pos = 0;
/* Enquanto o inicio não chegar até o meio do vetor, ou o meio do vetor
não chegar até seu fim, compara os valores entre o inicio e o meio,
verificando em qual ordem vai guarda-los ordenado.*/
while(i < meio && m < fim) {
/* Se o vetor[i] for menor que o vetor[m], então guarda o valor do
vetor[i] pois este é menor. */
if(vetor[i] <= vetor[m]) {
novoVetor[pos] = vetor[i];
pos = pos + 1;
i = i + 1;
// Senão guarda o valor do vetor[m] pois este é o menor.
} else {
novoVetor[pos] = vetor[m];
pos = pos + 1;
m = m + 1;
}
}
// Adicionar no vetor os elementos que estão entre o inicio e meio,
// que ainda não foram adicionados no vetor.
while(i < meio) {
novoVetor[pos] = vetor[i];
pos = pos + 1;
i = i + 1;
}
// Adicionar no vetor os elementos que estão entre o meio e o fim,
// que ainda não foram adicionados no vetor.
while(m < fim) {
novoVetor[pos] = vetor[m];
pos = pos + 1;
m = m + 1;
}
// Coloca no vetor os valores já ordenados.
for(pos = 0, i = inicio; i < fim; i++, pos++) {
vetor[i] = novoVetor[pos];
}
}
}- Na linha 70 declara a assinatura do método intercala que recebe o vetor e as posições inicio, meio e fim que serão ordenadas dentro do vetor.
- Na linha 84 tem um while que serve para ordenar os elementos do inicio ao meio do vetor, ou do meio ao fim do vetor.
- Na linha 101 tem um while que é para os elementos que estão no inicio do vetor, mas ainda não foram ordenados.
- Na linha 109 tem um while que é para os elementos que estão no meio do vetor, mas ainda não foram ordenados.
- Na linha 116 tem um for para passar os valores ordenados no vetor original.
Merge Sort usando recursão
/**
* Método que ordena um vetor de elementos inteiros, utilizando o algoritmo
* do Merge Sort.
*
* @param inicio - Posição inicial do vetor.
* @param fim - Posição final do vetor.
* @param vetor - Vetor de números inteiros.
*/
private static void mergeSortRecursivo(int inicio, int fim, int[] vetor) {
System.out.println("Inicio: " + inicio + " - Fim: " + fim);
/* Se o inicio for menor que o fim menos 1, significa que tem elementos
dentro do vetor. */
if(inicio < fim - 1) {
// Guarda a posição do meio do vetor.
int meio = (inicio + fim) / 2;
/* Chama este método recursivamente, indicando novas posições do
inicio e fim do vetor. */
mergeSortRecursivo(inicio, meio, vetor);
/* Chama este método recursivamente, indicando novas posições do
inicio e fim do vetor. */
mergeSortRecursivo(meio, fim, vetor);
// Chama o método que intercala os elementos do vetor.
intercala(vetor, inicio, meio, fim);
}
}- Na linha 25 tem a assinatura do método recursivo de merge sort, que agora recebe a posição inicial e final do vetor que será ordenado.
- Na linha 27 verifica se o inicio é menor que o fim – 1, para saber se o vetor não está vazio.
- Na linha 29 calcula a posição que seria o meio do vetor que será ordenado, está posição é utilizada para dividir o vetor e depois intercalar seus valores.
- Na linha 31 chama o método recursivamente, só que agora a posição final do vetor vai ser a posição do meio do vetor, que foi calculado anteriormente, assim faremos as chamadas recursivas caminhando para a esquerda do vetor.
- Na linha 35 chama o método recursivamente, só que agora a posição inicial vai ser a posição do meio do vetor, que foi calculado anteriormente, assim faremos as chamadas recursivas caminhando para a direita do vetor.
- Na linha 38 chama o método que vai intercalar (ordenar) os valores do vetor.
A imagem abaixo mostra a arvore de chamadas recursivas, caso este método receba um vetor de 5 elementos.

Em vermelho está a ordem em que os métodos serão chamados recursivamente.
Exemplo de Merge Sort com vetor de objetos
Neste exemplo temos uma classe Animal e cada animal tem uma especie e um nome.
package mergesort;
public class Animal {
private String especie;
private String nome;
public Animal(String especie, String nome) {
this.especie = especie;
this.nome = nome;
}
public String getEspecie() {
return especie;
}
public void setEspecie(String especie) {
this.especie = especie;
}
public String getNome() {
return nome;
}
public void setNome(String nome) {
this.nome = nome;
}
}A partir da classe animal, criamos um vetor de animais e queremos ordenar os animais pelo nome.

Segue abaixo a implementação do programa que ordena o vetor de animais pelo nome utilizando o algoritmo de Merge Sort:
package mergesort;
public class OrdenarAnimal {
public static void main(String[] args) {
Animal bidu = new Animal("Cachorro", "Bidu");
Animal fred = new Animal("Peixe", "Fred");
Animal rex = new Animal("Cachorro", "Rex");
Animal akamaru = new Animal("Cachorro", "Akamaru");
Animal mingau = new Animal("Gato", "Mingau");
Animal[] animais = new Animal[] {bidu, fred, rex, akamaru, mingau};
mergeSort(0, animais.length, animais);
for(int tamanho = 0; tamanho < animais.length; tamanho++) {
System.out.println("Especie: " + animais[tamanho].getEspecie() +
" - Nome: " + animais[tamanho].getNome());
}
}
/**
* Método que ordena um vetor de Animal, utilizando o algoritmo do
* Merge Sort.
*
* @param inicio - Posição inicial do vetor.
* @param fim - Posição final do vetor.
* @param vetor - Vetor de Animal.
*/
private static void mergeSort(int inicio, int fim, Animal[] animais) {
/* Se o inicio for menor que o fim menos 1, significa que tem elementos
dentro do vetor. */
if(inicio < fim - 1) {
// Guarda a posição do meio do vetor.
int meio = (inicio + fim) / 2;
/* Chama este método recursivamente, indicando novas posições do inicio
e fim do vetor. */
mergeSort(inicio, meio, animais);
/* Chama este método recursivamente, indicando novas posições do inicio
e fim do vetor. */
mergeSort(meio, fim, animais);
// Chama o método que intercala os elementos do vetor.
intercala(animais, inicio, meio, fim);
}
}
}O método do merge sort é muito parecido com o anterior, à única diferença é que na assinatura do método ele recebe um vetor de objetos Animal.
/**
* Método responsavel por intercalar os valores do vetor de forma ordenada.
*
* @param vetor - Vetor que terá seus valores ordenados.
* @param inicio - Posição inicial da ordenação no vetor.
* @param meio - Posição do meio da ordenação no vetor.
* @param fim - Posição final da ordenação no vetor.
*/
private static void intercala(Animal[] animais, int inicio, int meio, int fim) {
/* Vetor utilizado para guardar os animais ordenados. */
Animal novoVetor[] = new Animal[fim - inicio];
/* Variavel utilizada para guardar a posicao do inicio do vetor. */
int i = inicio;
/* Variavel utilizada para guardar a posição do meio do vetor. */
int m = meio;
/* Variavel utilizada para guarda a posição onde os
valores serão inseridos no novo vetor. */
int pos = 0;
/* Enquanto o inicio não chegar até o meio do vetor, ou o meio do vetor
não chegar até seu fim, compara os valores entre o inicio e o meio,
verificando em qual ordem vai guarda-los ordenado.*/
while(i < meio && m < fim) {
/* Se o vetor[i] for menor que o vetor[m], então guarda o valor do
vetor[i] pois este é menor. */
if(animais[i].getNome().compareToIgnoreCase(animais[m].getNome()) <= 0) {
novoVetor[pos] = animais[i];
pos = pos + 1;
i = i + 1;
// Senão guarda o valor do vetor[m] pois este é o menor.
} else {
novoVetor[pos] = animais[m];
pos = pos + 1;
m = m + 1;
}
}
// Adicionar no vetor os elementos que estão entre o inicio e meio,
// que ainda não foram adicionados no vetor.
while(i < meio) {
novoVetor[pos] = animais[i];
pos = pos + 1;
i = i + 1;
}
// Adicionar no vetor os elementos que estão entre o meio e o fim,
// que ainda não foram adicionados no vetor.
while(m < fim) {
novoVetor[pos] = animais[m];
pos = pos + 1;
m = m + 1;
}
// Coloca no vetor os valores já ordenados.
for(pos = 0, i = inicio; i < fim; i++, pos++) {
animais[i] = novoVetor[pos];
}
}O método intercala é muito parecido com o anterior, na assinatura do método linha 53, alterou o tipo do vetor que ele recebe, para receber um vetor de objetos Animal.
Na linha 55 cria um vetor de objetos Animal, para guardar temporariamente os Animais ordenados pelo nome. Na linha 70 foi alterado, para ordenar os nomes dos Animais em ordem crescente.
Conteúdos relacionados
- Ordenação de dados com Bubble Sort
- Ordenação de dados com Quick Sort
- Pesquisa sequencial
- Pesquisa binaria