Ordenação de Dados - Quick Sort

Quick Sort

Conceitos do QuickSort

O próximo algoritmo de ordenação de dados que falaremos é o Quick Sort. Assim como o Merge Sort, o Quick Sort é um algoritmo que se baseia no princípio da divisão e conquista, porem ele trabalha de maneira contrária uma vez que a parte mais pesada do algoritmo acontece antes da recursão e não nela.

O algoritmo Quick Sort trabalha ordenando uma sequência qualquer de valores dividindo-a em subsequências menores, aplicando recursão para ordenar cada uma destas subsequências e por fim, concatenando-as novamente em uma sequência idêntica a original, porem, já ordenada.

Divisão – Para uma sequência S de ao menos dois elementos, basta escolher um elemento x de S chamado por pivô. Uma vez feito isso, removemos todos os elementos de S e os alocamos em três novas subsequências, sendo elas:

• Uma subsequência Me, composta de elementos menores do que x.
• Uma subsequência Ig, composta de elementos iguais a x.
• Uma subsequência Ma, composta de elementos maiores do que x.

Vale lembrar que, caso exista apenas um elemento de valor igual ao de x, a subsequência Lg será composta de apenas um elemento.

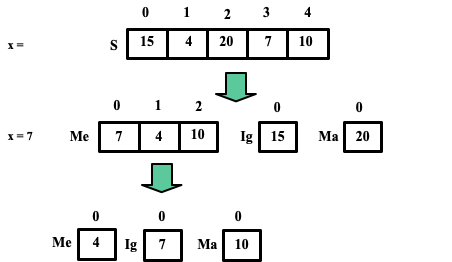
Recursão – Ordene as sequências Me e Ma recursivamente.

Conquista – Recoloque os elementos das subsequências Me, Ig e Ma novamente na sequência S nesta mesma ordem em que foram mencionados.

QuickSort in-place

Uma das melhores maneiras de se aplica o Quick Sort, é através da metodologia Quick Sort in-place. É dito in-place, pois não necessitará de novas sequências, ou seja, não necessita alocar mais memória.

Para que isto seja possível, iremos no preocupar não somente com a composição de novos vetores, mas sim iremos a partir do pivô comparar todos os elementos do vetor com o pivô de maneira a trocar elementos de posição e deixar o pivô centralizado, ou seja, com elementos menores que ele a sua esquerda e maiores que ele a sua direita, com isso já teremos os três novos vetores.

Para que isso seja possível, adotaremos a seguinte técnica:

• Escolher um elemento x do vetor, no caso o primeiro elemento do vetor;
• Percorrer o vetor da esquerda para a direita procurando um elemento maior que x, e da direita para a esquerda procurando um elemento menor ou igual a x. Quando este elementos forem encontrados, devemos troca-los de posição;
• Trocar x com o j-ésimo elemento e devolver a posição j.

Exemplo:

x = S[p] = 12

4 < 12? Sim -> incrementar ponteiro…

15 < 12? Não! -> parar ponteiro…

28 > 12? Sim -> decrementar ponteiro…

20 > 12? Sim -> decrementar ponteiro…

6 > 12? Não! -> parar ponteiro…

Os dois ponteiros pararam, logo os seus elementos devem ser trocados e ambos os ponteiros devem ser incrementados!

Continuando…

7 < 12? Sim -> incrementar ponteiro…

10 < 12? Sim -> incrementar ponteiro…

2 < 12? Sim -> incrementar ponteiro…

1 < 12? Sim -> incrementar ponteiro…

13 < 12? Não! -> parar ponteiro…

13 > 12? Sim -> decrementar ponteiro…

1 > 12? Não! -> parar ponteiro…

Uma vez que os dois ponteiros se ultrapassaram, o elemento escolhido x deve ser agora trocado com o elemento da posição j.

Essa foi a primeira passada percorrendo o vetor, o mesmo processo deve continuar até que o vetor fique completamente ordenado. O código a seguir apresenta como implementar o Quick Sort em Java.

Implementação do QuickSort in-place em Java

Para iniciar o exemplo, vamos criar uma classe QuickSort:

package quicksort;

/**
 * Classe utilizada para demonstrar o uso do algoritmo de ordenação
 * Quick Sort.
 */
public class QuickSort {
  /**
   * Método para a ordenação de um vetor de inteiros.
   * @param vetor - Vetor de inteiros que sera ordenado.
   */
  public void ordenarVetorDeInteiros(int[] vetor) {
    quickSort(vetor, 0, vetor.length - 1);
  }
}

A classe QuickSort já disponibiliza um método específico para a ordenação de números inteiros, conforme a linha 15 do código.

Note que este método invoca o método private void quickSort(int[] vetor, int inicio, int fim), logo vamos a seu código fonte:

  /**
   * Método que irá chamar a divisão do vetor nos três vetores do conceito.
   * Na realidade o vetor do meio esta sendo incarado apenas como o elemento
   * pivô retornado pelo método dividir.
   *
   * @param vetor - Vetor de inteiros que passara pelo Quick Sort.
   * @param inicio - Indice inicial do vetor que sera considerado no Quick Sort.
   * @param fim - Indice final do vetor que sera considerado no Quick Sort.
   */
  private void quickSort(int[] vetor, int inicio, int fim) {
    if(fim > inicio) {
      //Chamada da rotina que ira dividir o vetor em 3 partes.
      int indexPivo = dividir(vetor, inicio, fim);
      /* Chamada recursiva para redivisao do vetor de elementos menores
        que o pivô. */
      quickSort(vetor, inicio, indexPivo - 1);
      /* Chamada recursiva para redivisao do vetor de elementos maiores
        que o pivô. */
      quickSort(vetor, indexPivo + 1, fim);
    }
  }

Observe que nesta etapa, o algoritmo visa divider o vetor de entrada utilizando o método private int dividir(int[] vetor, int inicio, int fim), conforme a linha 32. Nesta etapa de divisão veremos como o algoritmo se comporta para realizar a ordenação a cada etapa desta divisão.

  /**
   * Método que ira dividir o vetor e encontrar o indice do pivô.
   * @param vetor - Vetor de inteiros
   * @param inicio - Indice inicial do vetor.
   * @param fim - Indice final do vetor.
   * @return O indice do pivo.
   */
  private int dividir(int[] vetor, int inicio, int fim) {
    int pivo, pontEsq, pontDir = fim;
    pontEsq = inicio + 1;
    pivo = vetor[inicio];

    while(pontEsq <= pontDir) {
      /* Vai correr o vetor ate que ultrapasse o outro ponteiro
        ou ate que o elemento em questão seja menor que o pivô. */
      while(pontEsq <= pontDir && vetor[pontEsq] <= pivo) {
        pontEsq++;
      }

      /* Vai correr o vetor ate que ultrapasse o outro ponteiro
        que o elemento em questão seja maior que o pivô. */
      while(pontDir >= pontEsq && vetor[pontDir] > pivo) {
        pontDir--;
      }

      /* Caso os ponteiros ainda nao tenham se cruzado, significa que valores
        menores e maiores que o pivô foram localizados em ambos os lados.
        Trocar estes elementos de lado. */
      if(pontEsq < pontDir) {
        trocar(vetor, pontDir, pontEsq);
        pontEsq++;
        pontDir--;
      }
    }

    trocar(vetor, inicio, pontDir);
    return pontDir;
  }

Este trecho de código responsável pela divisão do vetor em função da comparação por base de um vetor, estabelecido pelo elemento inicial do vetor, conforme a linha 63.

Utilizando dois ponteiros, um vindo da esquerda e outro da direita, este algoritmo ao mesmo que divide o vetor em dois novos vetores, estabelece uma ordenação fundamentada no pivô, onde os elementos menores que ele ficarão a sua esquerda e os maiores a sua direita. Quando elementos que não atendam a esta regra são localizados no vetor, estes são trocados pelo método private void trocar(int[] vetor, int i, int j), conforme linhas 79 e 84. Vejamos seu código fonte:

  /**
   * Método para trocar dois elementos de um vetor.
   *
   * @param vetor - Vetor de inteiros que tera seus elementos trocados.
   * @param i - Indice do elemento que sera trocado.
   * @param j - Indice do elemento que sera trocado.
   */
  private void trocar(int[] vetor, int i, int j) {
    int temp = vetor[i];
    vetor[i] = vetor[j];
    vetor[j] = temp;
  }

Agora, já finalizada a classe QuickSort, vamos elaborar uma classe de teste para ver o comportamento do algoritmo:

package quicksort;

public class TesteQuickSort {
  public static void main(String[] args) {
    int vetor[] = {24, 66, 87, 43, 11, 27, 4, 2, 7, 8, 4, 5,
     12, 53, 42, 22, 1, 5, 9, 13, 16, 23, 13, 7, 55, 67,
     92, 22, 33, 27, 19};

    QuickSort sort = new QuickSort();
    sort.ordenarVetorDeInteiros(vetor);
    imprimirVetor(vetor);
  }

  private static void imprimirVetor(int[] vetor) {
    System.out.println("Vetor...\n");
    for(int num : vetor) {
      System.out.print(num + ", ");
    }
  }
}

Conteúdos relacionados

• Ordenação de dados com Bubble Sort
• Ordenação de dados com Merge Sort
• Pesquisa sequencial
• Pesquisa binaria